The most commonly quoted statistics in investing are historical average investment returns. But are we talking about arithmetic means or geometric means of those returns, is it uniform across the industry and does it matter? It’s vital to understand this to analyse past results correctly.
First, some definitions:
- Arithmetic returns are the everyday calculation of the average. You take the series of returns (in this case, annual figures), add them up and then divide the total by the number of returns in the series.
- Geometric returns (also called compound returns) involve slightly more complicated maths. The geometric mean is calculated by multiplying all the (1+ returns), taking the n-th root and subtracting the initial capital (1). The result is the same as compounding the returns across the years.
The arithmetic mean can never be less than the geometric mean.
A simple way to explain the difference is by taking the numbers 2 and 8. The arithmetic average is 5, being (2 + 8)/2 = 10/2 = 5. The geometric mean, on the other hand, is 4: exactly 20 per cent lower. This is calculated as v(2 x 8) = v16 = 4.
The last 33 years of the S&P/ASX 200 accumulation index provides a relevant example of investment returns:
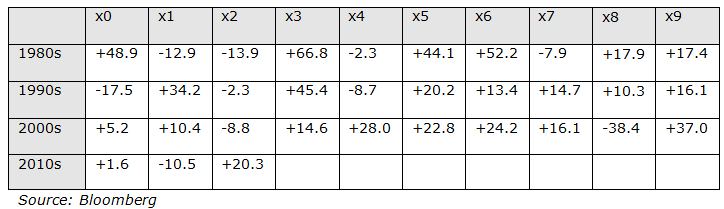
The arithmetic mean of these returns is 13.9% per annum. The geometric mean can be calculated from the index levels of 1000 on 31 December 1979 and 37,134.5 on 31 December 2012 and is 11.6% per annum. In other words, if the investment return were 11.6% every year from 1980 onwards, and you compounded the result, you would have grown your capital to the same extent as the index over the same period (ignoring cash flows, taxes, fees and so on).
This annual 2.3% gap between the arithmetic (13.9%) and geometric (11.6%) means is a big difference! If the index in fact grown at 13.9% each year compounded, it would have finished 2012 at 73,330.2, nearly double the actual value of 37,134.5.
Volatility, risk and average returns
The gap is caused by volatility. The more volatile a stream of investment returns, the greater the difference between the two measures. Let’s calculate the gap over two years for three hypothetical investment return scenarios:
- two years of zero returns (0, 0)
- up 10% in the first year and down 10% in the second (+10, -10)
- up 20% in the first year and down 20% in the second (+20, -20).
The arithmetic average of each of these scenarios is 0% per annum (over-weighting the effect of gains and under-weighting the effect of losses). The geometric mean of each is different, being:
- 0% per annum
- minus 0.5% per annum (your capital goes from 100 at the start to 110 in year one to 99 in year two, so you have lost money)
- minus 2.0% per annum (you have lost even more money).
If you are looking at a share investment, where the standard deviation of volatility can approach 20% per annum, the gap between arithmetic and geometric means can be significant. A 7.5% arithmetic average annual return, with 20% per annum volatility, will translate into a compound return of 5.9% a year (ie what actually ends up in your pocket over the longer term). This gap is what volatility costs the investor.
Not the risk premium
Don’t jump to the wrong conclusion that the gap is part of the risk premium. If you are comparing the returns on a risky asset with those of a risk-free asset, you need to consider the end result for both assets; that is, use the geometric return.
Any risk premium, which the investor demands to be paid to accept risk, needs to be above the compound return of the risk-free asset. Also, if you measure historical risk premiums (what was actually received) you should be careful to use compounding and not take a simple average.
The calculation of the historical risk premium can be problematic. Consider the same 33-year period from December 1979 until the end of 2012, this time for the return on Australian bond investments. Using a combination of the Commonwealth Bank Bond Index and the UBS Composite, bonds returned a compound 9.6% per annum over that period. The arithmetic average return was 9.9% per annum.
The trap for the unwary, in looking at the equity risk premium, is to calculate the return difference every year, and then average that risk premium. This is the same as estimating the equity risk premium from our 33-year sample period as 4.0% per annum (from 13.9 - 9.9 = 4.0) when it is only 2.0% per annum, using the geometric returns (11.6 – 9.6 = 2.0). If our sample 33-year period is anything to go by, this 2% is the risk premium that will compound over time.
The right set of scales for ‘weighing’ returns
Self-directed investors are well-advised to ask themselves, or their advisers, how their investments have performed over the preceding 12 months and longer periods of 3, 5 and 10 years (or longer). Take an SMSF trustee without access to the necessary advice or tools. How do they do this? If they compile a spreadsheet with each return from the relevant periods and then simply average them, chances are they are over-estimating their returns.
A point-to-point measure of how an index has moved over a 12-month period is what it is. However, it is easy enough for a self-directed investor to average these 12-month measures incorrectly (ie using a simple arithmetic mean) over multiple periods and, even worse, using the result to estimate future wealth accumulation.
Investing is a journey across many financial periods and calls for a way to ‘weigh’ those returns properly. The geometric mean is the appropriate set of scales for this job, at least until you look at the difference between time-weighted and money-weighted returns, but that is a topic for another day.
Aaron Minney is Head of Retirement Income Research at Challenger Limited. He was assisted in preparing this article by Senior Research Analyst, Liam McCarthy.